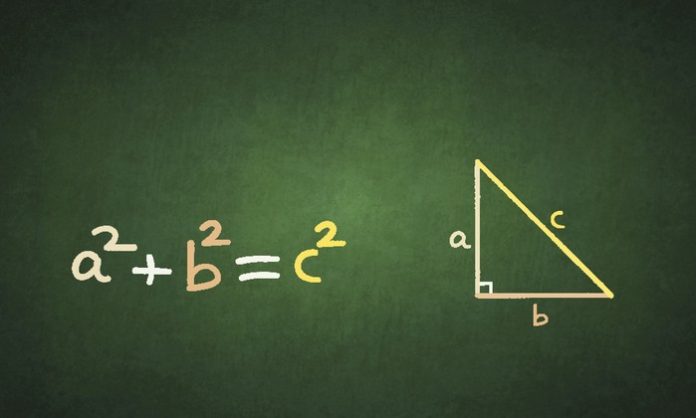Pythagoras menjadi salah satu rumus pada pelajaran matematika yang sangat sering digunakan hampir di setiap jenjang pendidikan.
Rumus Pythagoras ini ditemui salah satunya pada segitiga siku-siku. Berikut rumus Pythagoras segitiga siku-siku dan contohnya.
Namun, sebelum membahas lebih lanjut, ada baiknya jika pahami terlebih dahulu pengertian segitiga siku-siku yang menjadi akar dari munculnya rumus Pythagoras.
Pengertian Segitiga Siku-siku
Segitiga siku-siku menjadi salah satu bentuk segitiga yang memiliki karakteristik tertentu yang sangat berbeda dengan bentuk segitiga lainnya.
Segitiga siku-siku adalah sebuah segitiga di mana salah satu sudutnya membentuk sudut siku-siku atau 90 derajat.
Sudut siku-siku atau 90 derajat inilah yang membuat segitiga siku-siku berbeda dengan segitiga yang lain dan membuatnya mudah untuk dikenali.
Dilansir dari laman Cuemath, berikut penjelasan mengenai rumus Pythagoras segitiga siku-siku lengkap dengan contohnya.
Sejarah Rumus Pythagoras
Rumus Pythagoras digunakan untuk mengetahui nilai dari sisi hipotenusa atau sisi yang berseberangan dengan sudut siku-siku atau sisi miring.
Rumus yang juga dikenal dengan Teorema Pythagoras ini ditemukan oleh seorang filsuf sekaligus ahli Matematika asal Yunani, Pythagoras.
Meski rumus ini sudah banyak diketahui sebelumnya, namun Pythagoras-lah yang mampu membuktikan rumus ini dengan matematis.
Hal inilah yang membuat filsuf kelahiran 582 SM ini diakui sebagai penemu dari rumus yang dinamai sesuai dengan namanya tersebut.
Rumus Pythagoras segitiga siku-siku dan juga contohnya akan dijelaskan pada artikel ini.
Rumus Teorema Pythagoras
Rumus Teorema Pythagoras menyebutkan jika pada sebuah segitiga siku-siku abc, maka kuadrat sisi hipotenusa atau sisi miringnya sama dengan jumlah kuadrat dari sisi yang lain.
Jika sisi (a) dan (b) merupakan alas dan tinggi dari segitiga siku-siku, maka (c) merupakan sisi miring atau hipotenusanya.
Dengan demikian, bisa disimpulkan jika kuadrat sisi miring atau c sama dengan jumlah kuadrat sisi alas dan tingginya, a dan b.
Jika dituliskan dalam rumus, maka diperoleh rumus Pythagoras sebagai berikut:
c2 (kuadrat) = a2 (kuadrat) + b2 (kuadrat)
Pada rumus Pythagoras ini mengungkapkan adanya hubungan antara ketiga sisi pada segitiga siku-siku yang saling terikat.
Rumus Teorema Pythagoras ini juga mengungkapkan jika jarak terpendek dari kedua sisi (a) dan (b) bisa diketahui dengan menghitung sisi miring atau hipotenusanya yang disebut sisi (c).
Rumus Teorema Pythagoras ini juga merupakan salah satu rumus yang sangat penting bagi ilmu matematika, khususnya pada bab geometri.